Ett numeriskt exempel på beräkning av sannolikheten för en felklassificering
Låt oss anta att det sanna värdet för vattendraget är EK=0.72. Låt oss vidare nöja oss med att beräkna sannolikheten för att det blir klassat som ”måttligt eller sämre”. Det inträffar om det uppmätta värdet, benämnt skattningen, blir lägre än 0,7. För att skilja på sant och skattat värde betecknas det skattade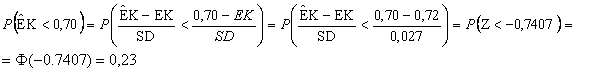
där Z=(
Bedömningen
För exemplet har indikatorn ASPT (Average Score Per Taxon) valts (helt godtyckligt). Den är indikator för ”Bottenfaunan i vattendrag” (en av flera). ASPT är medelpoängen för de familjer (av arter) som förekommer i vattendraget. För måluppfyllelsen används den ekologiska kvalitetskvotenVattendragets ASPT / Referensvärdet
där referensvärdet är ett värde på ASPT som indikerar en mycket hög kvalitet för ett vattendrag av den typ som är aktuell. I exemplet har valts vattendrag i boreala höglandet och då är referensvärdet 6,67. Poäng, referensvärde och nedanstående gränser är hämtade ur NV4, bilaga A, sidorna 67 och 68.
Kvaliteten på vattendraget ska nu med avseende på ASPT för bottenfaunan klassas som Hög, God, Måttlig, Otillfredsställande eller Dålig beroende på om EK-värdet är minst 0,9, mellan 0,7 och 0,9, mellan 0,45 och 0,7, mellan 0,25 och 0,45 eller under 0,25. Detta då med regeln ”direkt insättning” (face-value), som är den som tillämpas för Vattendirektivet i Sverige. Kvaliteten klassas alltså enligt det värde som erhålls vid provtagning.
Beräkning av sannolikheten för felklassificering generellt
Den generella (korrekta) beräkningsgången är följande. Det sanna värdet EK ligger i ett intervall med nedre gräns uL och övre gräns uH. För högsta kvaliteten är uH=∞ och för den lägsta är uL=-∞. En skattning betecknas som ovan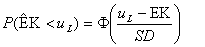
För sannolikheten att objektet hamnar i en högre klass erhålls på analogt sätt
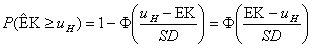
Totala sannolikheten för fel blir summan av dessa båda,
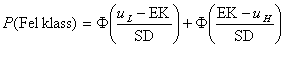
Formlerna stämmer även för ytterlighetsklasserna (Φ(-∞)=0 och Φ(∞)=1).
Funktionen Φ(t) är växande och eftersom både uL-EK och EK-uH är icke-negativa (och åtminstone en av dem är strikt negativ) så blir sannolikheten för felklassificering större ju större standardavvikelsen är. Man kan också (rent matematiskt) visa att sannolikheten blir minst om EK=(uL+uH)/2, d.v.s. för objekt med index mitt i klassen.
Det är enkelt att göra beräkningarna i Excel. Skriv in (sanna) EK-värden i en kolumn, säg i kolumn A. I kolumn B lägger vi sannolikheten att vi hamnar i en sämre klass och det får vi genom NORMSDIST((uL-Ax)/SD, där uL är nedre gränsen för den klass som ”hör” till EK. x i Ax är första raden med EK-värden. I kolumn C lägger vi sannolikheten för att hamna i en högre klass genom NORMSDIST((Ax-uH)/SD), där uH är övre gränsen för den klass som hör till EK. Värdet på SD är i vårt fall 0,027. Man får se upp med att uL och uH ändras ibland (vid byte av klass). Figur 1 visar en graf gjord i Excel med data genererade på detta sätt. I samma figur visas också motsvarande värden för regionen ”Centralslätten” (södra Sverige), där den högre variationen i bottenfaunan medför en högre standardavvikelse för skattningen, med SD=0.075 (gränserna mellan klasserna är desamma). I stället för NORMSDIST kan NORMDIST användas och då blir ”anropen” NORMDIST(uL;Ax;SD;SANT) respektive NORMDIST(Ax;uH;SD;SANT).
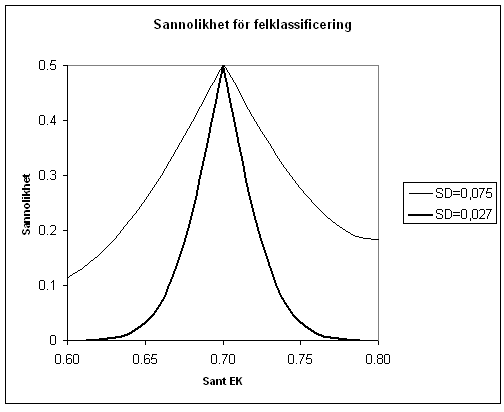
Figur 1. Sannolikheten för felklassificering av bottenfaunan för sanna värden på EK mellan 0,60 och 0,80. Tjock kurva (SD = 0,027) gäller för boreala höglandet. Tunn kurva (SD= 0,075) för Centralslätten (södra Sverige). (Normalfördelade avvikelser etc. förutsätts)
Grafen i NV4, sidan 58, är uppritad efter samma sorts beräkningar och härrör från Clarke et al. (den finns i artikeln från 1996).


