Redundancy Analysis (RDA) och Canonical Correspondence Analysis (CCA)
Beskrivning
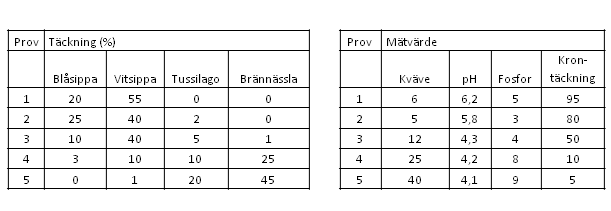
I de fall man har två set av data från varje prov, t.ex. artsammansättning och markkemi i provytor (Tabell 1), kan man kombinera dessa båda dataset för att direkt förklara variationen i artsammansättning med markkemivariablerna. Ett annat exempel kan vara att man vill förklara skillnader i vattenkemi mellan sjöar med hjälp av geografiska variabler. Beroende på vilket dataprogram man använder kallas dessa båda dataset för olika saker (Tabell 2).Tabell 1. Exempel på två olika typer av beskrivningsvariabler av fem prover. Till vänster arter (responsvariabler) och till höger miljöfaktorer (förklaringsvariabler) för samma prover som i tabellen till vänster.
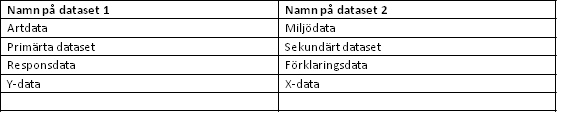
Tabell 2. Synonyma benämningar på de två dataset som används i multivariata metoder där man har både respons och förklaringsvariabler i samma analys.
Precis som för multivariata analyser på ett dataset (PCA/CA) finns det en metod för data med linjär respons och en metod för data med unimodal respons, läs mer här. Här är det responsen hos responsvariablerna eller Y-variablerna som avses. För analyser med responsdata med linjär respons används RDA och för responsdata med unimodal respons används CCA. Förklaringsdata kan ha linjär respons i båda metoderna.
Exempel
Här följer ett exempel med ordinationer på de båda dataseten ovan i tabell 1. Egentligen är dessa dataset för små för att en multivariat analys ska vara nödvändig, men resultatet är tydligt och principen för tolkning av denna typ av ordinationer framgår därmed också tydligt. Gemensamt för de båda metoderna är att de resulterar i ett ordinationsdiagram där både responsvariabler och förklaringsvariabler är illustrerade. Diagrammen tolkas så att de förklaringsvariabler med långa vektorer (pilar) är viktiga för de gradienter som återspeglas i ordinationsdiagrammet. Vidare talar vinkeln mellan en ordinationsaxel och vektorn för en förklaringsvariabel om sambandet mellan dessa: ju minder vinkel desto starkare samband. I figur 1 är således kväve den dominerande förklaringsvariabeln eftersom:- Den har den längsta vektorn
- Ligger närmast axel 1 (som alltid förklarar den mesta variationen i datasetet)
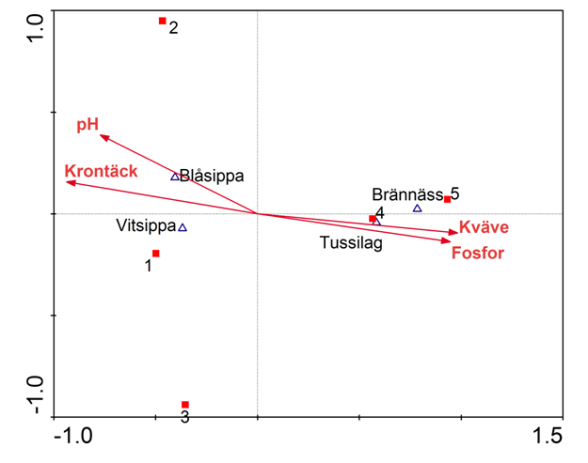
Figur 1. Resultat av en CCA (Canonical Correspondence Analysis) där både artdata och miljödata i tabell 1 använts i samma analys för att förklara mönster i artdata med de miljödata man uppmätt. Pilar representerar förklaringsvariabler, trekanter responsvariabler (växterna) och kvadrater proverna. I detta fall är kväve och fosfor viktigast för fördelningen av arter och prover längs den horisontella axeln. Fördelningen längs den vertikala axeln har ingen riktigt bra koppling till de använda förklaringsvariablerna, men pH har starkast inverkan bland de fyra förklaringsvariabler som ingår i denna analys.
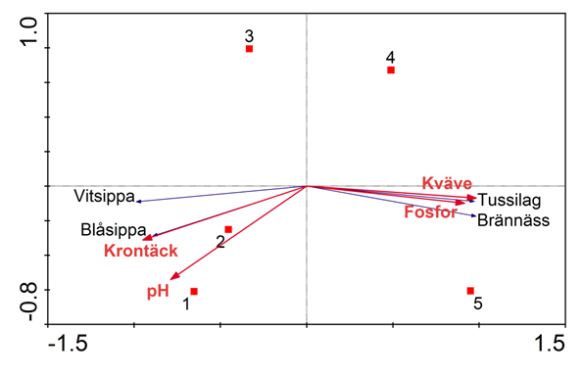
Figur 2. Analys av samma data som i figur 1, men här har RDA (Redundancy Analysis) använts. I detta fall blir resultaten liknande, men teoretiskt är RDA fel analys i detta fall då RA kräver linjär respons hos responsdata (växterna i detta fall). Största principiella skillnaden mellan CCA (Figur 1) är att responsvariablerna i RDA är representerade av vektorer (pilar).
Viktigt att veta
I denna presentation av metoderna är bara huvuddragen av metoderna presenterade för en basal förståelse av vad det handlar om. Likaså har vi bara gått in på den grafiska presentationen av resultaten. Det finna även olika metoder för att mer objektivt testa relevansen och signifikansen för de olika förklaringsvariablerna. Se Detaljer nedan för närmare information.Precis som för korrespondensanalys, CA, kan man råka ut för en s.k. ”arch effekt” även i CCA. Därför finns möjligheten att ta bort de eventuell ”arch effect” genom ”detrending” i metoden DCCA ”Detrended Canonical Correspondence Analysis”. Se diskussionen om detrending i avsnittet om CA för närmare beskrivning.
Fallgropar
Som redan nämnts ovan gäller det att använda rätt metod till den typ av data man har. Redan i de två exemplen ovan blir resultatet olika med de olika metoderna. I exemplet är det främst provernas placering i ordinationsdiagrammet som skiljer. Med större dataset kan resultaten skilja sig väsentligt. Precis som i PCA/CA gäller att proverna placeras i ett hästskoliknande mönster om man använder en metod som förutsätter linjär respons på data med unimodal fördelning. Detta framgår redan i exemplet i denna beskrivning (Figur 2).En annan fallgrop är problemet med relaterade förklaringsvariabler. Om flera av de variabler man använt som förklaringsvariabler är starkt korrelerade kan resultatet bli missvisande. Även fast två korrelerade variabler i princip säger samma sak kan det i ett ordinationsdiagram se ut som att en av dem förklarar mycket av variationen, medan den andra ser ut att har låg inverkan. Om inte det program man använder har en inbyggd varning för korrelerade variabler bör man testa detta innan man tolkar resultaten av en RCA/CCA analys.
Detaljer
Signifikansen eller relevansen för de förklaringsvariabler man inkluderat i en RDA/CCA kan testas med hjälp av olika tekniker. Detta bör också göras som ett komplement till den grafiska framställningen. Signifikanstestningen sker på lite olika sätt i olika program. Vi går inte in på detaljer kring detta här, utan hänvisar till respektive programs manual. En utförligare beskrivning finns också på The Ordination Web Page .Datorprogram
Denna typ av ordinationer finns bara i ett fåtal program främst ämnade för multivariat dataanalys av ekologiska data, t.ex.PC-Ord (kommersiellt)
Canoco (kommersiellt)
PAST (gratis)
R-modulen ”vegan” (gratis)
