PMF- Exempel 1
Det här är ett simulerat dataset. Det är 1 receptor och 4 källor. Varje källa har en gaussisk profil för sina emissioner, men med olika toppar. Över tiden faller emissionerna, men med olika tidskonstant. Litet brus är tillagt de rena signalerna.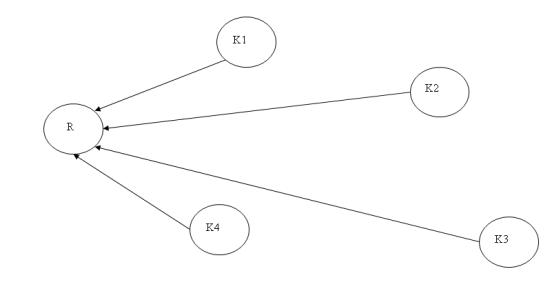
Figur 1: Struktur över emissionskällor och receptor
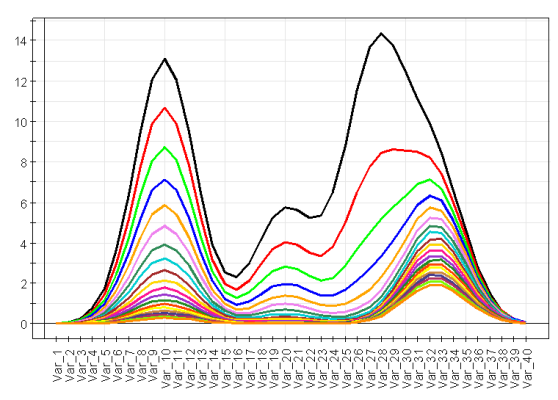
Figur 2: Emissionsspektrum med 40 kanaler 20 gånger över tiden.
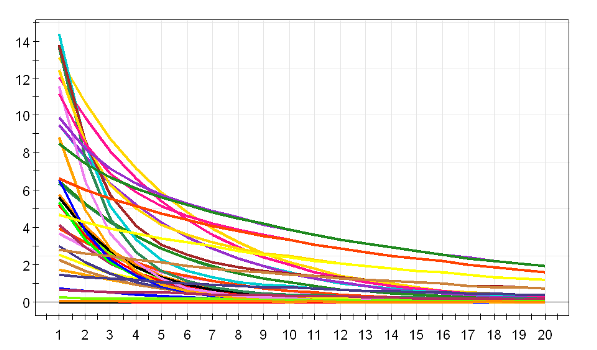
Figur3: Plot över varje kanal över tiden.
Här är data analyserade med PMF2. Data ligger i filen GE.DAT. Körinställningarna ligger i filen GE.INI PMF2 är ett DOS-program som beräknar F, G och E och lägger resultaten i olika filer. Vi har ställt in INI-filen så att summan av varje profil = 1.0. Analysen görs i 2 steg i programmet. Modellen är
X = G * F + E
Först söker programmet reda på en lösning G, F som ger bäst anpassning till data givet att alla element i F och G >= 0.0. Det söker den lösning som ger lägsta kvadratsumma av elementen i E. Modelleringsgraden kan man räkna ut som R2 = 1 – ss(E2) / ss(X2). Vi får R2 = 0.999. Sedan roteras lösningen roteras med hjälp av parametern FPEAK i INI-filen. FPEAK = 0.0:
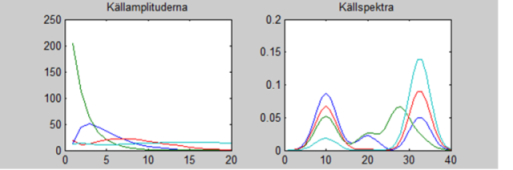
Figur 4: Källornas amplitud över tiden (vänster) och källornas profiler (höger). Dessa ser sammanblandade ut.
Figur 5: Vrider vi lösningen med att sätta FPEAK = -0.5 ser det bättre ut
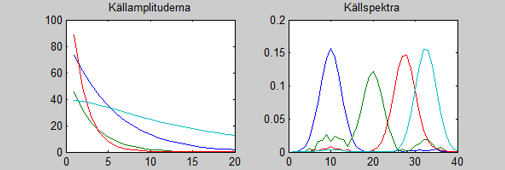
Figur 6: FPEAK = -0.9, ännu litet bättre, så som vi förväntat oss
Vi ser det exponentiella avtagandet för varje källa. Det spiller fortfarande över en aning från de båda mellersta källorna till de yttre i bilden. Bättre än så här får vi inte. Vider vi lösningen åt andra hållet blir det värre:
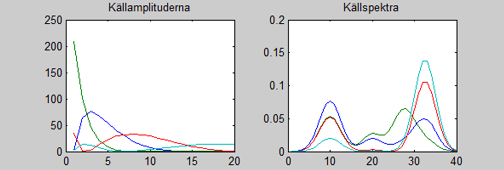
Figur 7: FPEAK = 0.5, en försämring
En slutsats är att man måste veta vad man söker efter.


