PLS - Exempel 1 - Analys av tobaksblad
Det här är ett klassiskt dataset med analysdata från tobaksblad, både oorganiska och organiska variabler. Det publicerades 1948 (W G Woltz et al 1948). Data finns i filen Tobak.xls. Data är analyserade med programmet SIMCA.I data finns 6 st oorganiska variabler: Totalkväve, Klor, Kalium, Fosfor, Kalcium och Magnesium, alla i [g/100g] I data finns också 3 ’organiska’ variabler: Brinnhastighet [tum/1000s], Socker [%] och Nikotin [%].
Det är 25 blad analyserade och frågeställningen är hur sambandet oorganiskt – organiskt ser ut.
PCA för översikt
Först gör vi en 2-komponenters principalkomponentanalys (PCA) för att få en överblick över data. Modellen förklarar 70% av variabiliteten i data.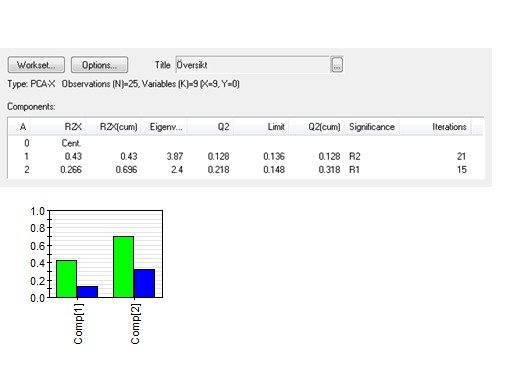
Figur 1: Förklarad variation i principalkomponentanalysen
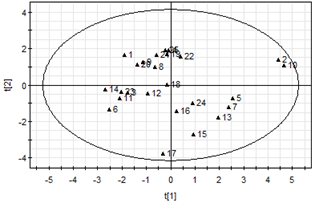
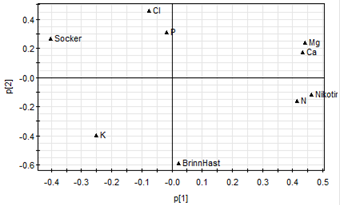
Figur 2: Scorebilden visar observationerna (ovan) och loadingbilden variablerna (nedan)
Observationerna ligger väl spridda i rymden, kanske obs 2 och 10 är litet annorlunda. Ellipsen visar det 95-procentiga konfidensintervallet för modellen, givet att data är approximativt normalfördelade. Med andra ord vore det normalt om 1 observation av våra 25 låg utanför ellipsen.
Våra ’responser’ ligger väl spridda från centrum i variabelbilden. Vi ser att Socker ligger diametralt motsatt nikotinet vilket antyder att de är negativt korrelerade. Brinnhastighet ligger rak ner och borde vara ganska oberoende av socker och nikotin. Nikotinet hänger ihop med Mg, Ca och N, så även socker fast med negativt tecken. Brinntid är mest korrelerad med kalium.
Med två komponenter som förklarar 70% av data har vi 30% av variabiliteten i residualen. Den kan vi visualisera per observation, observationernas avstånd till modelplanet, kallad DModX.
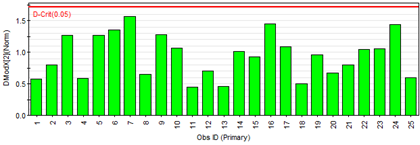
Figur 3: Observationernas avstånd till modelplanet (DModX).Vi ser ingen direkt avvikare, över den röda linjen (95-procentiga konfidensavståndet).
I och med att det inte finns några avvikare och att de organiska och oorganiska variablerna verkar sammanfalla i loadingbilden kan vi konstatera att data verkar vara utan konstigheter och att det finns samband mellan X och Y i data.
PLS för relationen
Vi gör nu en PLS-modell med de 6 organiska variablerna som X och de andra 3 som Y. Modellen beräknas med korsvalidering och får 2 komponenter som tillsammans förklarar 70% av variationen i Y.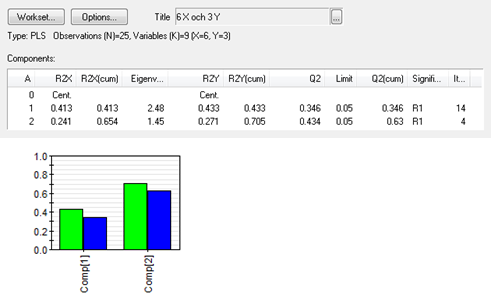
Figur 4: kumulativ modelleringsgrad (R2Y grön) och prediktionsförmåga (Q2 blå)
Bilden ovan visar kumulativ modelleringsgrad och prediktionsförmåga med 1 och sedan 2 komponenter. Skillnaden mellan modelleringsgrad och prediktionsförmåga får inte vara för stor, då är modellen överanpassad. Här har vi R2Y = 0.71 och Q2 = 0.63. En modelleringsgrad på 71% får anses bra i dessa sammanhang. Detta betyder att 71% av variationen i Y kan förklaras av de inkluderade X-variablerna. Differensen mellan R2Y och Q2 bör, enligt tumregel, inte vara större än 0.2. Q2 är alltid mindre än R2Y. För stor differens antyder att modellen är överanpassad till data och saknar matchande prediktionsförmåga.
Ovan ser vi kumulerad modelleringsgrad och prediktionsförmåga för alla Y tillsammans. Vi kan också se samma sak redovisad per Y-variabel med 2 komponenter.
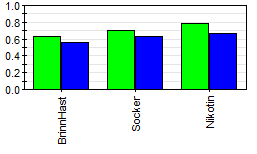
Figur 5: Kumulerat modelleringsgrad och prediktionsförmåga per Y-variabel med 2 komponenter Nikotinet (0.78/0.67) modelleras bäst, därefter socker (0.70/0.63) och sist brinnhastighet (0.63/0.56).
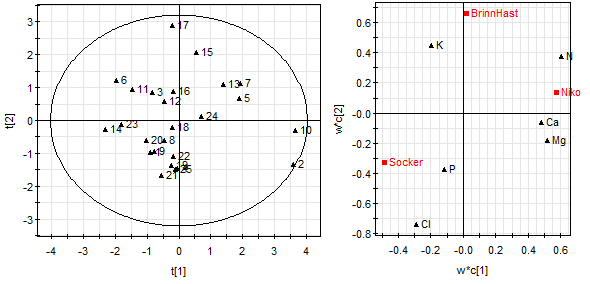
Figur 6: Scorebilden visar observationerna (vänster) och loadingsbilden variablerna (höger). Vi kan tolka bilderna: blad 17 har hög brinnhastighet, bladen i nedre delen brinner långsamt, blad 10 har högsta nikotinhat och lägsta sockerhalt.
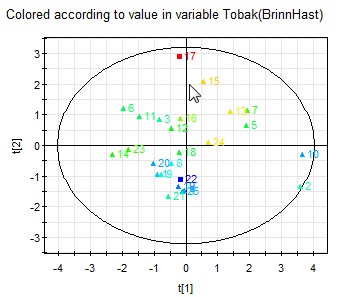
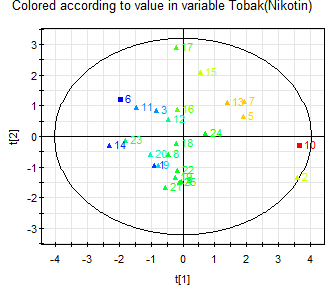
Figur 7: Scoreplotten är färgad efter Brinntid och Nikotin där rött innebär ett högre värde och blått ett lägre värde.
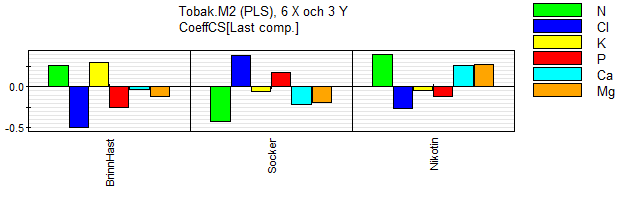
Figur 8: En PLS-modell kan också redovisas som koefficientbilder, en för varje Y-variabel.
I Figur 8 ser vi bilden för koefficienterna för de skalade X och Y-variablerna. Man ser att Cl är den viktigaste variabeln för brinntid (negativt inflytande). N dominerar för nikotinet. Kalium verkar inte ha något med socker eller nikotin att göra. Man får dock passa sig vid tolkningen av koefficienter eftersom X-variablerna normalt inte är oberoende. X-variablerna sitter ’fast’ i ett korrelationsmönster och det kanske inte går att bara ändra på en och hålla övriga konstanta (lägger man däremot upp variationen av X enligt en statistisk försöksplan så kan man tolka effekten av varje X för sig).
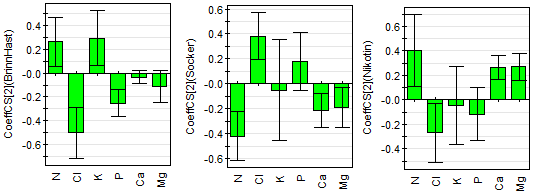
Figur 9: Med hjälp av korsvalideringen kan man beräkna approximativa konfidensintervall för koeffcienterna
Nästa steg efter att ha gjort en modell för alla Y och alla X är att fundera på om några X skall bort, och om man skall modellera Y i olika grupper. Det kan vara så att det i X finns helt irrelevanta variabler och att man genom att ta bort dem får en bättre modell.
I Figur 9 ser vi att koefficientbilden för Brinnhastighet är olik den för de två andra, vilka är varandras invers i stort sett. Kanske skulle vi här modellera Brinnhastighet i en egen PLS-modell och då utesluta Ca och Mg. I modell två skulle vi ha Socker och Nikotin och där exkludera Kalium. Gör man detta finner man att Brinnhastmodellen inte blir bättre (0.62/0.54), medan den andra blir något bättre (071/0.63 för socker och 0.79/0.65 för nikotinet)
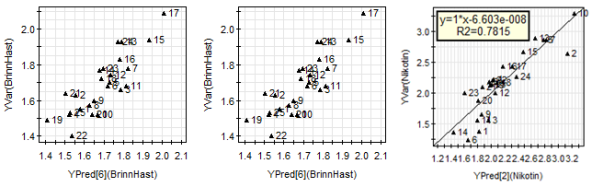
Figur 10: Bilder över observerade och predikterade värden. Korrelationskoefficienterna R2Y är de som redovisats ovan (0.63, 0.70 och 0.78)
Skulle det visa sig att något samband ser krökt ut kan det löna sig att prova med att transformera Y eller lägga till högre ordningens termer på X-sidan. Log(Y) är nog den oftast förekommande varianten.


